

Disfrute de millones de las últimas aplicaciones de Android, juegos, música, películas, TV, libros, revistas y más. En cualquier momento, en cualquier lugar, a través de sus dispositivos.
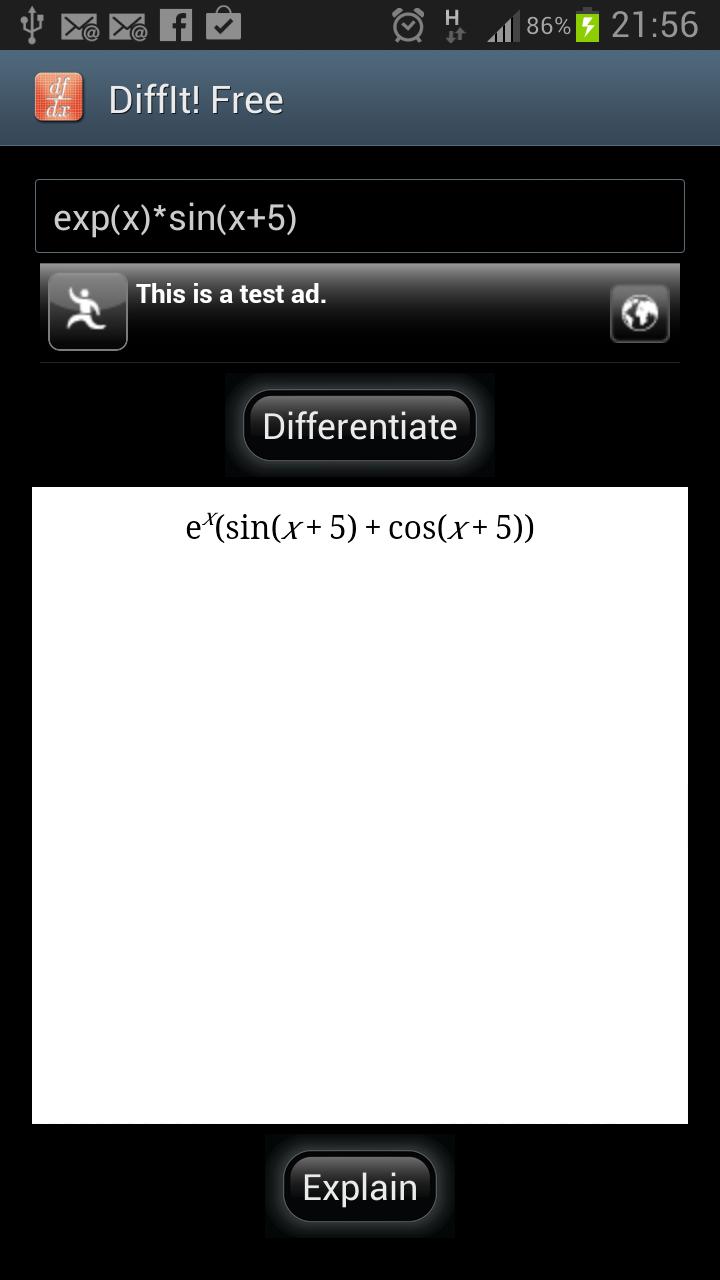
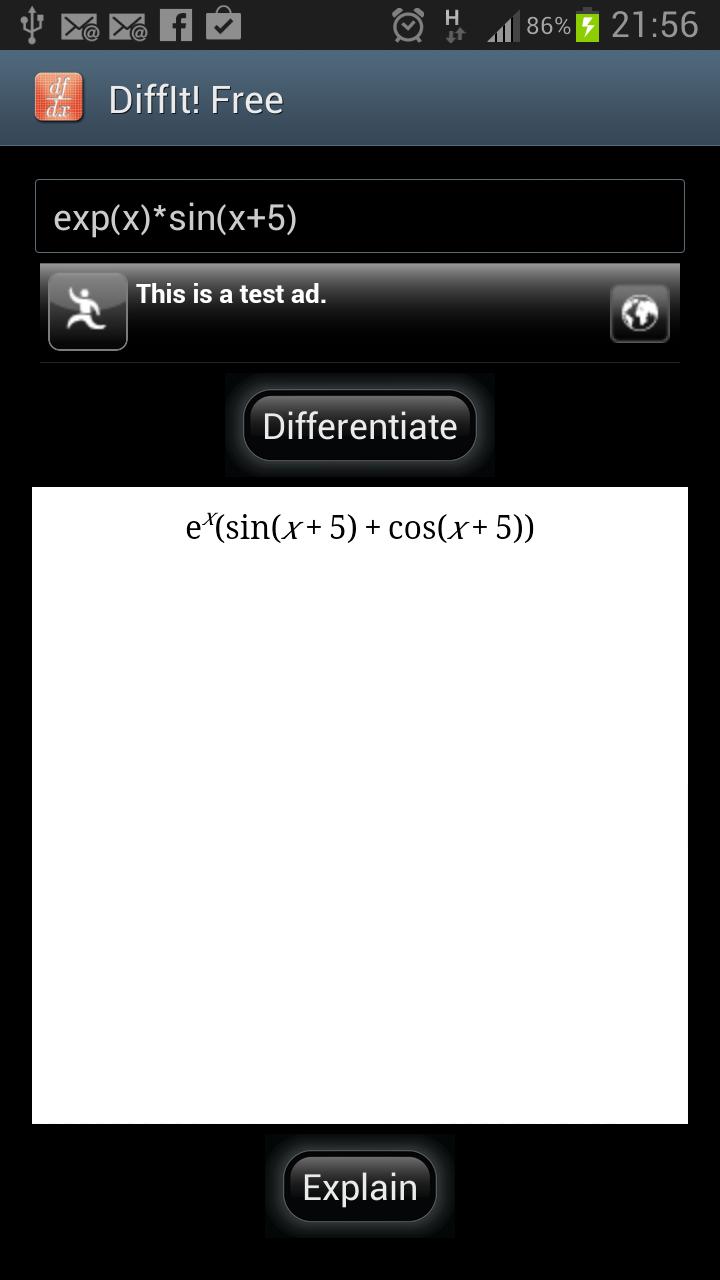
DiffIt! Free calcula y explica derivados de funciones matemáticas.
¡Escriba una función matemática y DiffIt! Free albedrío lo diferenciará. Además, puede decirle cómo llegó al resultado. La explicación traza todos los pasos y también le dice qué reglas se han aplicado.
Esta herramienta fácil de usar puede ayudarlo a aprender a encontrar derivados de las funciones más comunes.
Las funciones admitidas son:
SQRT EXP
pecado cos bronceado
asin acos atan
Sec cosec cot
Sinh Cosh Tanh
asinh acosh atanh
sech csch coth
LN log log2
Erf Erfc
DiffIt! Free es admitido por AD. Si le gusta esta aplicación y desea deshacerse de la publicidad, ¡admitirnos y comprar la versión completa llamada Diffit!
Cambios en la versión 1.1.4
- Se corrigió el error de entrada vacío
- Se corrigió el error de análisis; Las expresiones no válidas se detectan de manera más confiable
- reglas de análisis modificadas; sin (x)^2 ahora se interpretará como (sin (x))^2
Tenga en cuenta que el sin x^2 ahora también se interpreta como (sin (x))^2, debe escribir sin (x^2) para una interpretación alternativa.
Cambios en la versión 1.1.3
- Diseño mejorado de botones
- El botón de retroceso y la barra de acción funcionan de acuerdo con las pautas
Cambios en la versión 1.1.1
- Error de enlace corregido
Cambios en la versión 1.1.0
- El análisis mejorado "sin x" es ahora una abreviatura aceptable de "pecado (x)"
- Se agregaron texto de ayuda y complete una referencia de las reglas de diferenciación
- Se corrigió un error de diálogo de bienvenida
- Simplificación de expresión mejorada